Introduction
The Jewish calendar is important to historians and genealogists because Jewish vital records use the Jewish dates. This includes not only birth, marriage, and death certificates, but tombstone inscriptions as well.
The Jewish calendar is both a solar and lunar calendar, with the months being synchronized to the moon, and years to the sun. As such, the rules governing the calendar can be a bit daunting. By contrast, the secular calendar we are all familiar with is purely a solar calendar with the months falling where they may. And the Moslem calendar, on the other hand, is a lunar calendar with the years falling where they may. So each of those calendars has only one heavenly body to worry about, whereas the Jewish calendar has two.
This paper presents the Jewish calendar in an easy-to-understand—and sometimes tongue-in-cheek—fashion as seen through the eyes of Adam and Eve. But in spite of the levity, the details presented are factual. The aim is not to make you an expert in calculating Jewish dates (we have programs to do that) but rather to give you an appreciation for what is involved in such calculations.
There are many myths surrounding the Jewish calendar. As an example, I once heard a lecturer say that that the reason all Jewish holidays start at sundown is because they are based on a lunar calendar. I hope to debunk such myths and, at the same time, perhaps create a few myths of my own.
In the Beginning
In the beginning God created the universe in six days. And on the seventh day He rested.
On the eighth day, Adam looked at Eve and said, “We need a calendar.” And Eve said “A what?” And Adam replied, “Let me explain. One day we are going to have children. Don’t ask me how we’ll do that—I’ll surprise you one night. But the important thing is that our children will have children and that will be the first family tree.”
And Eve said, “What’s a tree?”
And Adam replied, “That’s not important. What’s important is that one of our children’s children will become a genealogist.” And Eve said “Oh, is he going to help us when we have the children?” Adam said “No, that’s a gynecologist.”
And Adam added, “We’re not going to live forever. I probably won’t make it much past my 930th birthday. It will be up to our genealogist grandchild to record the years that we lived, so that future generations will know. In order to do that, he’ll need a way of counting years and months. That’s what the calendar is all about.”
Counting Years and Months
Adam was very astute, and he noticed that the days were growing longer. Then he noticed that they started growing shorter, and then after a while they started growing longer again. And he said to Eve, “I’ll bet that has something to do with the sun.”
And he noticed that the water on the beach was getting higher each day. Then it started getting lower, and it too repeated. And he said to Eve, “I’ll bet that has something to do with the moon.”
Eve was getting the picture now, and she said, “Adam dear, let’s use the sun to count years and the moon to count months.” And so they did.
Each time the earth made one revolution around the sun they called it a year. And each time the moon made one revolution around the earth, they called it a month.
But then they noticed that there wasn’t an exact number of months in a year—it was somewhere between 12 and 13. So Adam said, “One of our grandchildren will be a mathematician, and he’ll invent fractions so we can handle this.” And Eve said, “Oh, is he going to slow down the moon so there’ll be exactly 12 months in a year?” And Adam said, “No that would be a magician.”
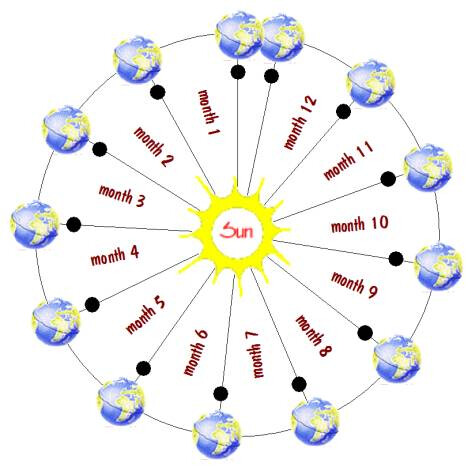
The diagram below shows the position of the earth relative to the sun after each revolution of the moon. Note that after 12 such revolutions, the earth is slightly shy of its original position. And after one more revolutions it will overshoot that position. It is this fact that makes it so difficult to have a calendar that is synchronized to both the sun and the moon at the same time. We will return to this problem later in the paper and see how the issue can be resolved.
Counting Hours
“And it was evening and it was morning, the first day.” So the first day (and every day thereafter) starts with a period of darkness and ends with a period of light.
Although the day starts at sundown, for mathematical purposes we assume that the day starts at 6 PM and count the hours as follows:
Hour 0: 6 PM Hour 6: midnight Hour 12: 6 AM Hour 18: noon
Hour 1: 7 PM Hour 7: 1 AM Hour 13: 7 AM Hour 19: 1 PM
Hour 2: 8 PM Hour 8: 2 AM Hour 14: 8 AM Hour 20: 2 PM
Hour 3: 9 PM Hour 9: 3 AM Hour 15: 9 AM Hour 21: 3 PM
Hour 4: 10 PM Hour 10: 4 AM Hour 16: 10 AM Hour 22: 4 PM
Hour 5: 11 PM Hour 11: 5 AM Hour 17: 11 AM Hour 23: 5 PM
The Effect of the Moon
Each month starts when the moon comes closest to being between the earth and the sun. This is called the new moon, or molad in Hebrew. And the time between molads is one month.
By careful measurements, it was found that the time between molads is almost exactly 29 days, 12 hours, 44 minutes, 3 1/3 seconds. So rather than observing the heavens to determine when the molad occurs, this time period became the definition of a month. If we know when any molad occurs, we can compute the precise time of every other molad from creation up until the end of time by repetitively adding or subtracting the above time period. So this time period is very important and forms the whole basis of the mathematical definition of the Jewish calendar. Make it your mantra – 29 days, 12 hours, 44 minutes, 3 1/3 seconds!
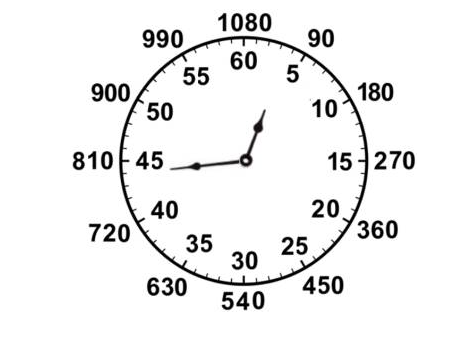
But working with fractional seconds is awkward. So instead of dividing the hour into minutes and seconds, let’s divide it into parts (halaqim in Hebrew) where there are 1080 halaqim in an hour. This means that a haliq (singular) is 3 1/3 seconds. Now the definition of a month becomes 29 days, 12 hours, 793 halaqim.
The diagram below shows an hour divided into both 60 parts (minutes) as well as 1080 parts (halaqim). And the minute hand in the diagram shows where 44 minutes 3 1/3 seconds (and its equivalent of 793 halaqim) would be.
The Effect of the Sun
Nineteen solar years are almost exactly 235 lunar months, differing by only a couple of hours. It was this discovery that allowed the calendar makers to resolve the problem mentioned earlier of not having an integral number of months in a year. They divided the 19-year cycle into 235 months, with some years having 12 months and others having 13. The breakdown is as follows:
Year 1: 12 months Year 11: 13 months (leap year)
Year 2: 12 months Year 12: 12 months
Year 3: 13 months (leap year) Year 13: 12 months
Year 4: 12 months Year 14: 13 months (leap year)
Year 5: 12 months Year 15: 12 months
Year 6: 13 months (leap year) Year 16: 12 months
Year 7: 12 months Year 17: 13 months (leap year)
Year 8: 13 months (leap year) Year 18: 12 months
Year 9: 12 months Year 19: 13 months (leap year)
Year 10: 12 months Total: 235 months
So in each 19-year cycle there are 12 common years and 7 leap years. The diagram below presents the same information in a graphical form.

This 19-year cycle is not unique to the Jewish calendar. It is used also in the Chinese calendar, the ancient Greek calendar, and in the calculations of Easter. Such a cycle is called a Metonic cycle after the Greek astronomer Meton.
Let’s name the months and arbitrarily assign the number of days in a month as follows
COMMON YEAR LEAP YEAR
Tishri (30 days) Tishri (30 days)
Heshvan (29 days) Heshvan (29 days)
Kislev (30 days) Kislev (30 days)
Tevat (29 days) Tevat (29 days)
Shevat (30 days) Shevat (30 days)
Adar 1 (30 days) Adar
Adar Adar 2 (29 days) Adar 2 (29 days) Veadar
Nisan (30 days) Nisan (30 days)
Iyyar (29 days) Iyyar (29 days)
Sivan (30 days) Sivan (30 days)
Tamuz (29 days) Tamuz (29 days)
Ab (30 days) Ab (30 days)
Elul (29 days) Elul (29 days)
This means that a common year has 354 days and a leap year has 384 days
Note that there is only one Adar in a common year, namely Adar 2. So that is often referred to as simply Adar. In a leap year there are two Adars, namely Adar 1 and Adar 2, and they are often referred to as Adar and Veadar. That can be the source of confusion if you are not careful about it. Plain Adar in a common year has 29 days and in a leap year has 30 days. This point is brought home when you think about the holiday of Purim, which occurs on the 14th day of Adar 2—Purim occurs in the 29-day month, regardless of whether it is a leap year.
In Hebrew, Adar 1 and Adar 2 are referred to as Adar Aleph and Adar Bet.
When Does the Year Start?
If I asked you that about the secular year, you would probably say January 1. And you would be correct as far as the calendar year is concerned (i.e., the time at which the year number changes). But what about the school year? It starts at the beginning of September, and school calendars typically go from September 1 to August 31. And there’s the fiscal year that can start at anytime, as selected by individual companies to simplify their yearly bookkeeping. Also there was the Julian year (no longer used today) in which the year started in March, resulting in September, October, November, and December being the 7th, 8th, 9th, and 10th months as their names imply.
The same is true for the Jewish year. The Jewish calendar year starts on Tishri 1 (Rosh Hashanah) and that is when the year number changes. But in biblical times, tree tithes (taxes) were assessed on each person based on the amount of fruit he harvested during the preceding year. The year for tree tithes started in Shevat. And animal tithes were assessed based on each person’s livestock holding for the year starting in Elul. And finally there was the king’s year, as each king’s reign began in the month of Nisan.
The choice of Nisan for the year start goes deeper than just the king’s reign. It is the start of the year for religious purposes. In Exodus 12:2, the passage regarding Passover reads: “This month [of Nisan] shall be to you the beginning of months; it shall be the first in the months of the year.”
The Drift of Tishri 1
Recall that one month (the period between molads) is 29 days, 12 hours, 793 halaqim. Thus the elapsed time for a common year (12 months) is 354 days, 8 hours, 876 halaqim, and for a leap year (13 months) is 383 days, 21 hours, 589 halaqim.
But based on the days we previously assigned to each month, a common year is 354 days and a leap year is 384 days. So a common year as defined by the calendar is 8 hours, 876 halaqim too short, and a leap year is 2 hours 491 halaqim too long. That will eventually cause Tishri 1 to come a day before or a day after the molad of Tishri.
The solution is to increase or decrease the number of days in a year to prevent Tishri 1 from drifting. To increase the number of days in a year, we add a day to the month of Heshvan. Such a year is called a complete year. And to decrease the number of days in a year, we subtract a day from the month of Kislev. That is a defective year. If a year is neither complete nor defective, it is called a normal year.
defective normal complete
year year year
Heshvan 29 29 30
Kislev 29 30 30
Common year 353 354 355
Leap year 383 384 385
And with that we have a working calendar. We could stop now and all would be well. But, alas, the religion comes into play, and we have to add some additional rules to satisfy religious constraints.
[Second thoughts: Since there are more common years than leap years, and since the common year’s deficiency is greater than the leap year’s excess, the only correction necessary is to increase the number of days. So from the standpoint of the drift, there is need for a complete year but not a defective year. However defective years will be needed in order to satisfy the four rules that are presented in the next section.]
The Four Rules
And Eve said, “Adam, please don’t let Yom Kippur fall on a Friday, because then I won’t be able to prepare food for Saturday, and we’ll have to fast for two days.”
And Adam replied, “I can do that by prohibiting the new year from starting on a Wednesday.”
The reason that works is shown by the following calendar image. In it you can see that if the new year (Tishri 1) started on a Wednesday, then Yom Kippur (Tishri 10) would indeed fall on a Friday

And Eve added, “Adam, please don’t let Yom Kippur fall on a Sunday, because then I won’t be able to prepare food for the break-fast, and we’ll go to bed hungry.”
And Adam replied, “I can do that by prohibiting the new year from starting on a Friday.”
The following calendar image shows that if the new year started on a Friday, then Yom Kipper would indeed fall on a Sunday.

And Eve said, “One more thing. Don’t let the last day of Succoth (Hashanah Rabbah) fall on a Saturday because then we won’t be able to beat the willow twigs.”
And Adam replied, “Beat the what? OK, OK, I’ll prohibit the new year from starting on a Sunday too. Will that make you happy?”
And here’s the calendar image showing that the only way for Hashanah Rabbah, Tishri 21, to fall on a Saturday is if the new year started on a Sunday.

But Adam dear, how will you prohibit the new year from starting on those days?”
“That’s simple. I’ll delay Tishri 1 by one day.”
And Eve asked, “Adam, just how do you plan on delaying Tishri 1 by a day?”
And Adam replied, “That’s easy. I’ll add one day to the month of Heshvan in the preceding year.
And that gets us to the first rule:
Rule 1: If molad Tishri occurs on Sunday, Wednesday, or Friday, delay Tishri 1 by one day.
And then Adam said, “Perhaps I better not let Tishri 1, the first day of the year, finish before the new crescent moon is visible.”
And Eve asked “Why?” And Adam replied, “I don’t know. It just sounds like the right thing to do.”
So here’s the second rule:
Rule 2: If molad Tishri occurs at 18 hr (i.e., noon) or later, delay Tishri 1 by one day.
And Eve said, “But Adam, what happens if your second rule (18 hr rule) and your first rule (Wed-Fri-Sun rule) both apply? Wouldn’t that require a delay of two days and might that make the previous year too long or the current year too short?”
And Adam replied “That’s a good point. Let’s figure out the conditions under which that could happen, and introduce some rules to prevent it.”
So the next two rules are:
Rule 3: If molad Tishri in a common year falls on Tuesday at 9 hr, 204 hq or later, delay Tishri 1 by one day.
Rule 4: If molad Tishri following a leap year falls on Monday at or after 15 hr, 589 hq, delay Tishri 1 by one day.
But these two rules, as worded, are too complicated. So let’s simplify the wording to the following:
Rule 3 (simplified): If a common year would be 356 days (one day too long), delay Tishri 1 by one day.
Rule 4 (simplified): If a leap year would be 382 days (one day too short), delay Tishri 1 of the following year by one day.
The Missing Piece
We know how many months (molads) are in each year.
We know the time between molads (28 days, 12 hours, 793 halaqim).
Can we figure out when the molad Tishri occurred in each year?
Yes, if we know when the first molad Tishri occurred.
So that gets us to a discussion of the origin of time, and determining when the first molad Tishri actually occurred.
The Origin of Time
And Adam said to Eve, “We need some origin from which to start counting years. It was just a week ago that God said ‘Let there be light’ and it was the first day. So let’s call that first day Tishri 1 in the year 1.”
And Eve replied, “But Adam, so much has happened in that week. We got day and night, heaven and earth, and all the animals in the zoo. That’s enough for a whole year. So let’s start the second year with the first day of rest. We’ll call that Tishri 1 in the year 2, and that whole creation thing can be the last week of year 1.”
Adam couldn’t figure out what happened to all the other weeks in year 1, but he didn’t want to argue and he let Eve have her way.
And the mathematicians were happy with this. For they knew from their calculations that the molad of Tishri in the year 2 was at 8 AM on Friday, the day Adam and Eve were created. And the mathematicians knew that year 2 couldn’t start on that Friday (otherwise Yom Kippur would be on a Sunday), so Tishri 1 in the year 2 would be delayed to Saturday, the first day of rest.
And so the calendar for the first year and the beginning of the second is as follows. Note that an extra day has been added to the month of Heshvan in year 1 to prevent year 2 from starting on a Friday. The circled days are the six days of creation.

But then Adam said, “Hey, we were just created, and we haven’t had a chance to sin yet. After all, there’s nobody out there for us to commit adultery with. We don’t need a day of atonement, so there’s no reason to delay Tishri 1 to Saturday.” So the Talmudic scholars decreed that the Friday on which Adam and Eve were created shall be Tishri 1 in the year 2. And who are we to argue with Talmudic scholars?
So the picture for years 1 and 2 is changed to the following and year 2 indeed starts on a Friday.

Six Thousand versus Fifteen Billion
Those of us who have studied science have been taught that the universe was created in the Big Bang some fifteen billion years ago. But the story of creation says that everything started not quite six thousand years ago. Now that’s quite a discrepancy – a difference of fourteen billion, nine hundred ninety-nine million, nine hundred ninety-four thousand years. Or, to put it another way, a 2.5 million percent error. How can this be?
One popular explanation has to do with the actual time taken for creation—those six circled days in the calendar above. It was six days, to be sure, but how long were those days? They were the periods between the start of one darkness and the start of the next darkness. Was that 24 hours, the time from sunset to sunset? How could it be since the sun wasn’t created until the fourth day? So they might have been very long periods of time and in total added up to fifteen billion years. A far-fetched theory, and possibly an after-the-fact rationalization, but it does bring the biblical and scientific theories into compliance.
However there’s an explanation that I like even better. When Adam and Eve were created, they were not infants crawling around on the ground. They were full-grown adults, or so the story in Genesis implies. So why should we think that the rocks and mountains and fossils were pristine? They too could have been aged at the time they were created to give all appearances of having been around for billions of years. In other words, there was an initial condition to this freshly created universe that made it look like it was billions of years old. We got a used universe! Perhaps even a recycled one that the creator had lying around from some previous experiments. It certainly brings everything into perspective.
A 689,472-Year Cycle
Warning: This section uses arithmetic. If that’s a problem, you can skip over it.
We’ve already seen that the Jewish calendar is based on a 19-year cycle. Does that mean that the calendar repeats itself every 19 years? Well as far as the pattern of leap years and common years goes, that is true.
But what about the pattern of defective, normal, and complete years? That will repeat only if the time of the molad of Tishri repeats itself. So how many cycles will it take for the molad of Tishri to once again occur at the same time that it started with?
To answer that question, let’s compute the time between the start of two consecutive 19-year cycles. Such a cycle consists of 235 months, and the time between the new moons of two consecutive months is 29 days, 12 hours, and 793 halaqim. Multiplying that out, we find that a 19-year cycle takes 6,939 days and 17,875 halaqim.
Since there are 25,920 halaqim in a day (1,080 times 24), the 17,875 halaqim represents a fractional day. So we need to accumulate enough cycles in order for the fractional days to add up to an integral number of days. The fraction is 17,875/25,920, which reduces to 3,575/5,184. In just 5,184 cycles, the fractional days will add up to exactly 3,575 days. And 5,184 cycles is 98,496 years (19 times 5,184).
So now we know that if we start at a molad of Tishri and wait 98,496 years, the next molad Tishri will occur at precisely the same time as the first one. Does that mean that the calendar will repeat after that? No, not yet. Recall that the rules of the calendar depend on the day of the week that the molad Tishri occurs. So the calendar will repeat only if both the time of the molad Tishri and the day of the week of the molad Tishri repeat.
Does the day of the week repeat after 98,496 years? No, because if we add up the number of days in 98,496 years we get 35,975,351 days (5,184 times 6,939 plus 3,575), which is not divisible by 7. But if we wait until 7 of these 98,496-year cycles pass, we would get back to the same day of the week and the calendar would completely repeat itself. And 7 times 98,496 is only 689,472 years!
Relating to Secular Calendar
The secular calendar in common use today is the Gregorian calendar. The rules for determining the number of days in each Gregorian year are simple and well known (365 for common years, 366 for leap years, a leap year being any year that is divisible by 4 except that if it is divisible by 100 it must also be divisible by 400 to be a leap year). Prior to the Gregorian calendar, the calendar in common use was the Julian calendar. It differed from the Gregorian calendar in that it did not have the century rule. And when the switch was made from the Julian to the Gregorian calendar, several days were skipped over to correct the accumulated error up to that time.
We know how to calculate the number of days since Tishri 1 in the year 1 for any Jewish date. To convert to secular dates, the only additional piece of information that we need is the secular date corresponding to Tishri 1 in the year 1. That turns out to be October 7, 3761 B.C.E. (before the common era) in the Julian Calendar, and for the Gregorian calendar the date turns out to be September 7, 3761 B.C.E.
Of course we previously said that Tishri 1 in the year 1 didn’t exist, and that creation didn’t start until the month of Elul in that year. But that shouldn’t prevent us from counting the days from this fictitious date. Of course if you wanted to be a purist, you could count the days from Tishri 1 in the year 2, the day Adam and Eve were created. So for you purists, the corresponding Julian date is September 26, 3760 B.C.E. and the Gregorian date is August 27, 3760 B.C.E.
Jewish Calendar Creep
The Jewish calendar is slowly creeping through the years. That is, the start of the Jewish year is occurring a little later each year relative to the seasons. This amounts to one-day every 217 years. Since we are nearly in the Jewish year 6,000, the calendar has already crept about 28 days since the time of creation. And in just 40,000 years it will creep six months so that instead of having Rosh Hashanah in the fall, we will have it in the spring. But fear not—in 80,000 years it will have crept a full year so that by the time the Jewish year 86,000 rolls around, our children’s children will once again celebrate Rosh Hashanah just before Halloween.
The reason for the creep is that the ratio of the Earth’s revolution around the sun (one year) to its rotation on its axis (one day) is not an integer. To put that another way, there are not an integral number of days in a year. The creep is caused by the inaccuracy in the value of this ratio as used in the Jewish calendar.
Here’s the calculation. The Jewish calendar is based on a 19-year cycle consisting of 235 lunar months. Each lunar month is defined as being 29 days, 12 hours, 793 halaqim.
Therefore the average number of days in a year is:
(235*(29 days + 12 hours + 793 halaqim)) / 19 =
(6,939 days + 16 hours + 595 halaqim) / 19 =
6,939.6896/19 days =
365.2468 days
The actual ratio, as determined by astronomical calculations, is 365.2422 days per year. That means that the average Jewish year exceeds an astronomical year by 0.0046 days. Therefore the Jewish calendar will creep one day every 1/0.0046 years, which calculates to 217 years.
Besides the Jewish years creeping through the seasons, the Jewish months are creeping through the phases of the moon, with each month starting a little later. The reason for this creep is the error in the definition of the time from one new moon to the next. The Jewish calendar is based on that time being 29 days, 12 hours, 793 halaqim, which comes to 29.530594135 days. But more precise astronomical calculations have shown that number to be 29.530588853 days. The error is 0.000005282 days/month, or 1 day every 15,776 years. That means that every 236,652 years, the start of the month will creep by 15 days, so by the year 237,000 the month will start with the full moon instead of the new moon.
Secular Calendar Creep
We know that the Julian calendar is creeping, and it was the accumulated creep of around 11 days that caused it to be discarded in favor of the Gregorian calendar. The ratio of days/year is based on a four-year cycle and comes to 365.25. Since the true astronomical ratio is 365.2422 days, the average Julian year exceeds the astronomical year by 0.0078 days, which means a creep of one day every 1/0.0078 years, which is 128 years. That’s almost twice as much creep as the Jewish calendar.
Even the Gregorian calendar is not correct and the seasons are creeping each year but at a much slower rate than the Julian or Jewish calendars. The ratio of days/year for the Gregorian calendar is based on a 400-year cycle with 365 days each year plus an extra day every 4 years minus no extra day in year 100, 200, and 300. Therefore the average number of days in a year is:
(400*365 + 100 - 3)/400 = 365.2425
That exceeds an astronomical year by 0.0003 days. Therefore the seasons in the Gregorian calendar will creep one day every 1/0.0003 years, which calculates to 3,333 years. In 600,000 years the accumulated creep will be 180 days, and we will have winter in July in the northern hemisphere. What a chilling thought.
Hebrew Numerals
The dates of death found on Jewish tombstones are encoded using a Hebrew equivalent of Roman numerals. In particular, the encoding is as follows:
1 א (aleph) 10 י (yud) 100 ק (kuf)
2 ב (bet) 20 כ (kaf) 200 ר (resh)
3 ג (gimel) 30 ל (lamed) 300 ש (shin)
4 ד (dalet) 40 מ (mem) 400 ת (tav)
5 ה (heh) 50 נ (nun) 500 תק (tav kuf: 400+100)
6 ו (vav) 60 ס (samekh) 600 תר (tav resh: 400+200)
7 ז (zayin) 70 ע (ayin) 700 תש (tav shin: 400+300)
8 ח (khet) 80 פ (peh) 800 תת (tav tav: 400+400)
9 ט (tet) 90 צ (tsadi) 900 תתק (tav tav kuf: 400+400+100)
An alternate encoding from 500 to 900 involves the final (sufit) letters as follows. This is not commonly used.
500 ך (final khaf)
600 ם (final mem)
700 ן (final nun)
800 ף (final feh)
900 ץ (final tsadi)
Starting at 1000, numbers are broken into two parts separated by an apostrophe. To the right of the apostrophe is the number of thousands and to the left is the number of units, both using the encoding shown above. Sometimes the thousands part is omitted completely.
5,699 תרצט ‘ה (heh apostrophe tav resh tsadi tet)
5,761 תשסא ‘ה (heh apostrophe tav shin samekh aleph)
This use of apostrophe can be extended to millions, billions, etc. Some examples are
1,000 ‘א (aleph apostrophe )
1,010 י ‘א (aleph apostrophe yud )
1,100 ק ‘א (aleph apostrophe kuf )
10,000 ‘י (yud apostrophe )
100,000 ‘ק (kuf apostrophe )
1,000,000 ‘‘א (aleph apostrophe apostrophe )
1,002,003 ג ‘ב‘א (aleph apostrophe bet apostrophe gimel )
10,000,001 א ‘‘י (yud apostrophe apostrophe aleph )
Usually a quotation mark is inserted just before the last (leftmost) character to make it clear that this is a number and not a Hebrew word. So 5,699 would be written as:
5,699 תרצ"ט ‘ה (heh apostrophe tav resh tsadi quote tet)
Although dates are usually written in a decimal notation (that is, one character representing the units column, another the tens column, etc.), this rule is sometimes violated just as long as the sum of the characters represents the desired result. For example, 15 would be written as yud (10) heh (5) in decimal notation. But these two letters are contained in the name of God, so the equivalent tet (9) vav (6) is usually used instead. Same goes for 16 which is usually written as tet (9) zayin (7) instead of yud vav.
15 טו (tet vav)
16 טז (tet zayin)
Examples of Hebrew Numerals:
Besides the obvious places (vital records, tombstones, etc), Hebrew numerals keep popping up all the time. Here is a picture of a clock in my house that has the numbers written as Hebrew numerals. The 1 through 10 are represented by the Hebrew letters aleph through yud. The 11 and 12 are yud aleph and yud bet.

The following is the familiar Jewish chai, which means life in Hebrew. It is traditionally associated with the number 18. Why? Because the letters in the word chai are khet (8) and yud (10). Normally 18 would be written yud khet, but the ordering is not crucial and chai is an equivalent Hebrew-numeral representation of 18.

WOW!!! That’s very interesting! It’s quite long… I’ll have to read it as chapter book